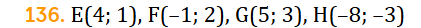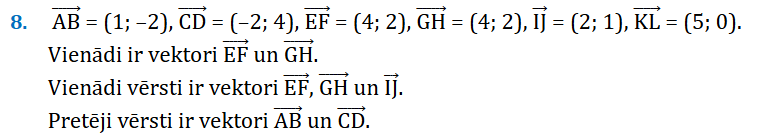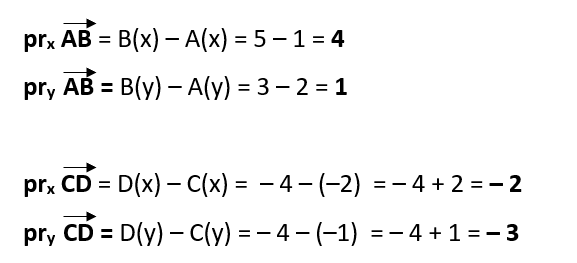1. stunda - iepazīšanās
1_stunda_1k_24_25.pptx
2. stunda
SR. Atpazīst skalārus un vektoriālus lielumus, zina, kas ir vektors un kā to apzīmē. Nosaka vienādi vai pretēji vērstus vektorus, vienādus vektorus, pretējus vektorus, ja tie doti ģeometriskā formā. Aprēķina vektoru garumu.
1. Ko Jūs jau zināt par vektoriem vai kādas ir radušās asociācijas izdzirdot šo jēdzienu "VEKTORI"?
2. Skatīsimies Tavaklase.lv piedāvāto video, pildot uzdevumus un salīdzinot ar tur dotajiem rezultātiem: Tavaklase.lv - Vektora jēdziens
3. Veidosim pierakstos konspektu:
1_1Skalari_un_vektoriali_lielumi.ppt
3. stunda
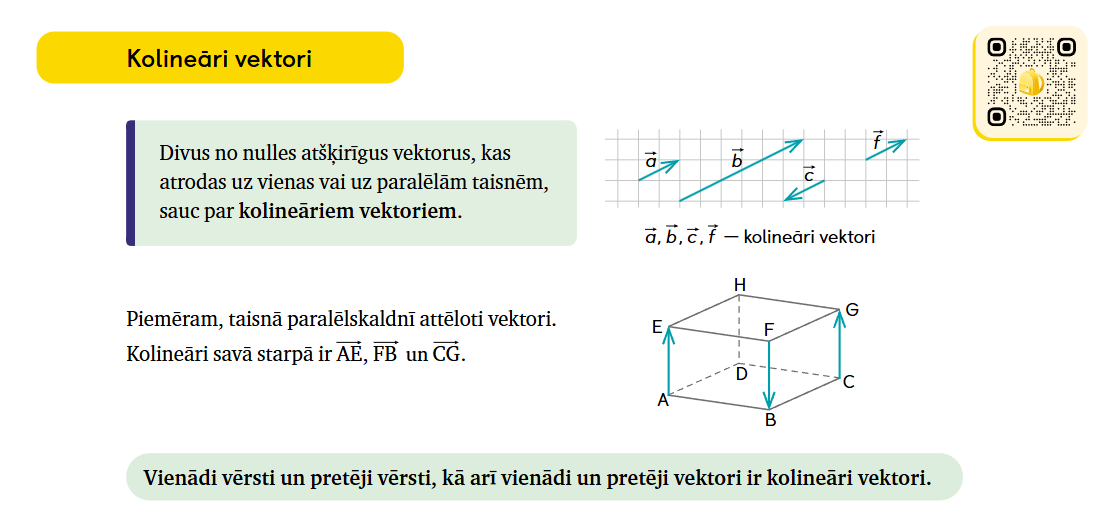
SR. Atpazīst kolineārus vektorus, ja tie doti ģeometriskā formā.
1. Atkārtojam, ko atceramies no iepriekšējās stundās apgūtā:

2. Pierakstos ierakstām informāciju par kolineāriem vektoriem.
3. Pildām uzdevumus no mācību grāmatas: 3. (10.), 5., 6., 7., 8., 9., 11., 12., 13., 14. (11.); 16.- 10. (12.)...
4. Novērtējam, cik labi esam apguvuši pamatzināšanas par vektoriem:
Patiesiba_vai_meli.ppt
Darbs uzdevumi.lv
4. stunda
SR. Saskaita vektorus izmantojot trijstūra likumu.
Veidojam konspektu par vektoru saskaitīšanu. Māc. gr. 16. - 18.lpp.
5., 6. stunda
SR. Uzzīmē divu vektoru summas vektoru, izmantojot trijstūra likumu un paralelograma likumu. Pieraksta divu vektoru summas vektoru.
1. Pildām uzdevumus no mācību grāmatas: 30., 29., 32., 33. (19.)
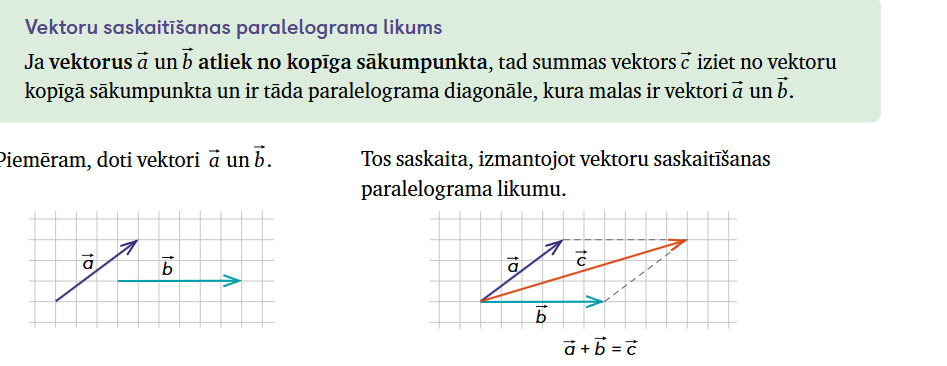
2. Veidojam konspektu par vektoru saskaitīšanas paralelograma likumu. Māc. gr. 17.lpp.
3. Pildām uzdevumus no mācību grāmatas: 29., 34. (19.)
7., 8. stunda
SR. Uzzīmē divu vektoru starpības vektoru. Pieraksta divu vektoru starpības vektoru.
1. Pierakstos ierakstām informāciju par vektoru atņemšanu:

|

2. Pildām uzdevumus no mācību grāmatas: 35., 38., 39., 40., 41., 42. (21. - 22.)
9. stunda (2.10.)
SR. Reizina vektoru ar skaitli
1. Pierakstos ierakstām informāciju par vektoru reizināšanu ar skaitli
2. Pildām uzdevumus no mācību grāmatas: 58., 59., 61. (29.)
3. Skolēni atkārto apgūto, pārskatot SR un pierakstus:
- Kuri no dotajiem lielumiem ir skalāri, kuri vektoriāli lielumi
- Nosauc zīmējumā redzamos vektorus
- Pieraksta vektora garumu
- Nosauc vienādus, pretējus, vienādi vērstus, pretēji vērstus, kolineārus, nekolineārus vektorus
- Uzzīmē prasītos vektorus (vienādu dotajam, pretēju dotajam, vienādi vērstu, pretēji vērstu dotajam)
- Uzzīmē doto vektoru summas vektoru, izmantojot trijstūra likumu un paralelograma likumu, pieraksta atbilstošu izteiksmi
- Izmatojot doto zīmējumu, pieraksta summas vektoru
- Uzzīmē doto vektoru starpības vektoru, pieraksta atbilstošu izteiksmi
- Nosaka skaitli, ar kuru jāreizina viens vektors, lai iegūtu citu vektoru
- Uzzīmē vektoru, kas ir dotā vektora reizinājums ar skaitli, pieraksta atbilstošu izteiksmi
10. stunda (2.10.)
Formatīvās vērtēšanas darbs: skalāri un vektoriāli lielumi, vektoru veidi, vektoru garums, vektoru saskaitīšana, atņemšana, reizināšana
11., 12. stunda (9.10.)
SR. Attēlo vektora projekcijas uz koordinātu asīm. Nosaka vektora projekcijai atbilstošo skaitli (atbilst projekcijas garumam)
1. Izvērtējam iepriekšējā stundā rakstītā formatīvās vērtēšanas darba rezultātus
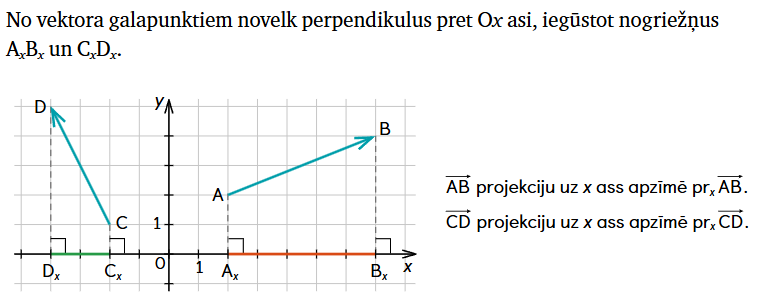
2. Veidojam konspektu par vektora projekcijām uz koordinātu asīm (MG 36.lpp.)

Lai iegūtu vektoru projekciju uz x ass
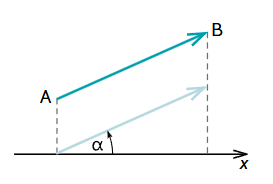 |
Vektora projekcija uz x ass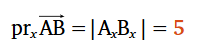 | Ja vektors vērsts "pa labi" - vērtība ir pozitīva |
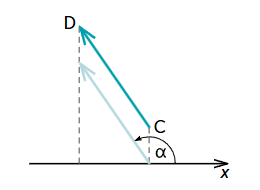 | 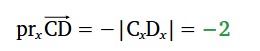 | Ja vektors vērsts "pa kreisi" - vērtība ir negatīva |
Lai iegūtu vektoru projekciju uz y ass

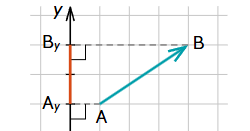 | Vektora projekcija uz y ass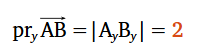 |
Ja vektors vērsts "uz augšu" - vērtība ir pozitīva |
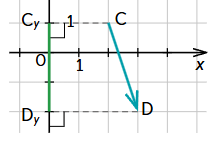 | 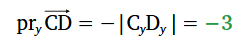 |
Ja vektors vērsts "uz leju" - vērtība ir negatīva |
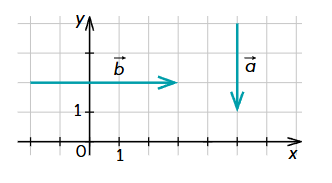 | 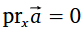 Vektora projekcija uz y ass ir negatīva | 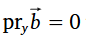 Vektora projekcija uz x ass ir pozitīva |
2. Pildām uzdevumus no mācību grāmatas: 88.(38.), 89., 90., 91., 93.
13., 14. stunda (16.10.)
SR. Aprēķina vektora projekcijas uz koordinātu asīm. Uzraksta vektora koordinātas
1. Atkārtojam, kā nosaka vektora projekcijas lielumu un pildām soma.lv viedgrāmatas uzdevumus paškontrolei
2. Pārzīmē zīmējumu. Parādi zīmējumā vektoru projekcijas. Uzraksti zīmējumā doto vektoru projekcijas
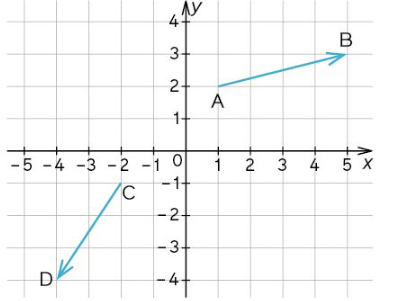
3. Mācāmies aprēķināt vektora projekcijas, salīdzinām ar zīmējumā nolasītajiem lielumiem
Lai aprēķinātu vektora projekcijas, no vektora galapunkta koordinātas atņem vektora sākumpunkta koordinātu
4. Mācāmies pierakstīt vektora koordinātas.

|
Pārzīmē zīmējumu. Pieraksti zīmējumā doto vektoru koordinātas.
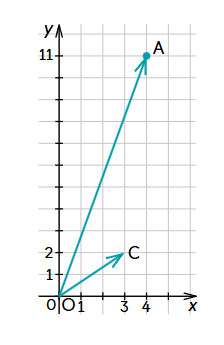
Ja vektora sākumpunkts neatrodas koordinātu sākumpunktā, vektora koordinātas ir šī vektora attiecīgās projekcijas skaitlis.

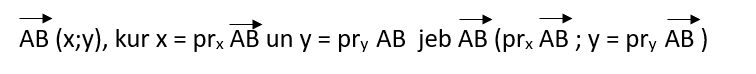
Ja |
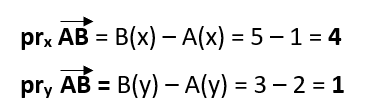
|
tad |
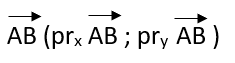
| tātad | 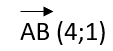 |
Uzdevums: Pieraksti katra zīmējumā dotā vektora koordinātas MG 53.lpp.:
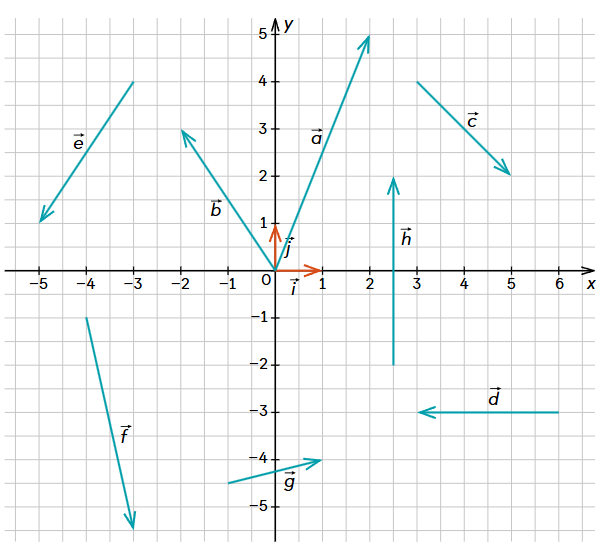
Uzdevumi no MG 135. (54.), 140., 145.
15., 16. stunda (23.10.)
SR. Izpilda darbības (saskaita, atņem, reizina ar skaitli) ar vektoriem koordinātu formā
1. Atkārtojam, kā aprēķina vektora koordinātas
2. Mācāmies izpildīt darbības ar vektoriem koordinātu formā: veido konspektu MG 58.lpp., izpēta 5. piemēru 59.lpp.
3. Pildām uzdevumus MG: 157. (59.), 161. (60.), 163., 164., 165.
Uzzīmē piemērus: 161. (d); 163. (e, g)
17., 18. stunda (24.10.)
SR. Aprēķina garumu (moduli) vektoriem koordinātu formā
1. Mācāmies aprēķināt garumu vektoriem koordinātu formā: veido konspektu MG 56.lpp., izpēta 3. piemēru.
3. Pildām uzdevumus MG: 148. (57.), 151., 150., 99. (43.), 103., 107.
19., 20. stunda (30.10.)
SR. Veic darbības ar vektoriem telpā
Pārrunājam formulas no eksāmena formulu lapas.

1. Patstāvīgi veic konspektu par vektoriem telpā: MG 64. - 65. lpp.
2. Risina uzdevumus MG 179., 180., 181.
3. Izpēta, kā saskaita vektorus, kas doti izmantojot paralēlskaldni: MG 1.piemērs 66.lpp.
4. Risina uzdevumus MG 182., 183., 184., 185., 186.
5. Izpēta, kā aprēķina vektora garumu telpā: MG 70.lpp.
6. Risina uzdevumus MG 196., 197.
21., 22. stunda (6.11.)
SR. Pārliecinās par gatavību pārbaudes darbam
1. Iepazīstas ar pārbaudes darba izpildei nepieciešamajām zināšanām un prasmēm
2. Interaktīvs treniņš pārbaudes darbam grupās
3. Patstāvīgi risina piemērus un noskaidro, kādas zināšanas un prasmes jānostiprina: Saturs (teorija); Risinām kopā (skaidrojumi pa soļiem); Risini pats (3.; 4a, b; 6.); Pārbaudi sevi.
Interaktīvās apmācības disks - Matemātika 10. klasei
Papilduzdevumi:
1.
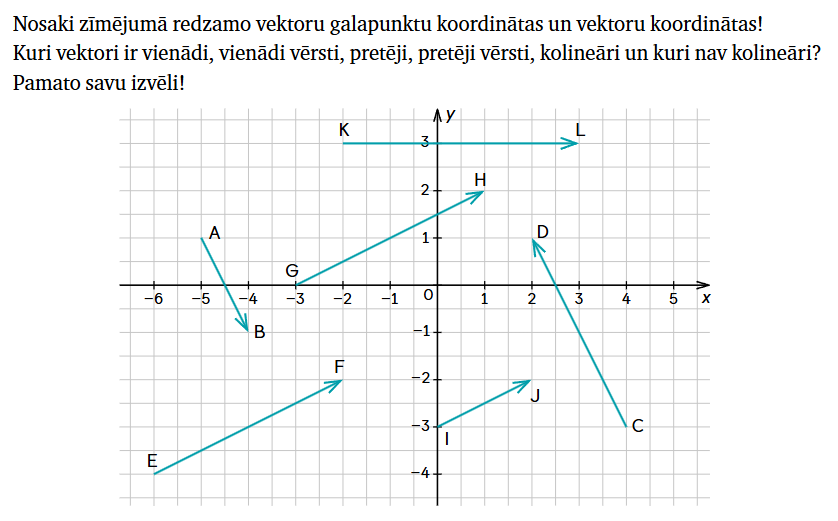
2.
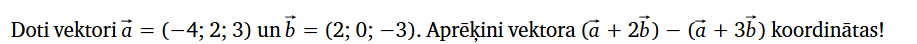
3.