1. stunda - 10. janvāris
SR. Nosaka, vai dotā sakarība ir funkcija
1. Iepazīstamies ar funkcijas definīciju
2. Pierakstām x un y dažādos nosaukumus
3. Iepazīstamies ar funkcijas uzdošanas veidiem (soma.lv 112.lpp.)
4. Pildām MG uzdevumus: 4.1., 4.2., 4.3., 4.4., 4.7. (176.); 4.28., 4.29. (183.)
2. (1.) - no 13. janvāra
PD rezultāti un kļūdas
SR. Atpazīst ar grafiku uzdotu funkciju
1. Atkārtojam, kādas sakarības sauc par funkcijām
2. Nosakām, kurā no zīmējumiem attēlota funkcija, izmantojot funkcijas definīciju
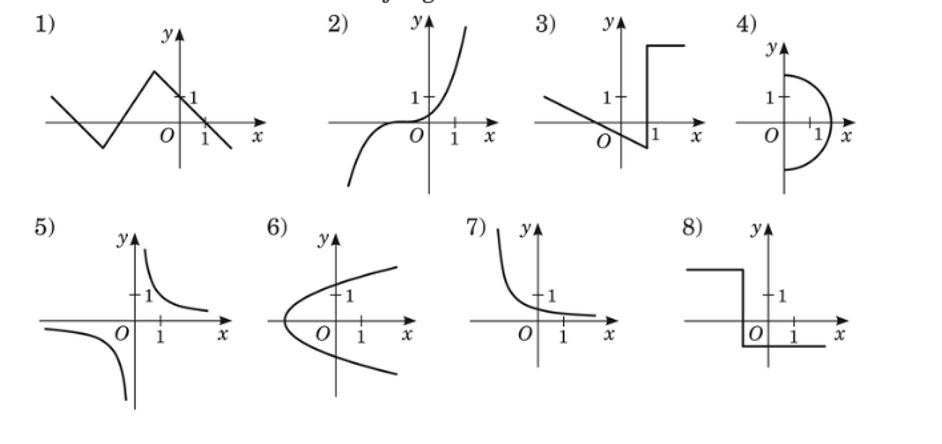
3. Pildām MG 4.28., 4.29. (183.), pārzīmējot grafikus un parādot, kāpēc dotais grafiks ir vai nav funkcionāla sakarība.
3. (2.)
SR.
Izmantojot grafiku, nosaka
x vērtībai atbilstošo y vērtību un
y vērtībai atbilstošo x
1. Pildām uzdevumus DL
2. Skolēni pilda uzdevumu MG 4.31. (184.)
5. (4.)
SR. Iepazīstas ar lineāru funkciju, tās grafiku un formulu. Nosaka lineārās funkcijas koeficientu k un b vērtības. Nosaka, vai dotais punkts pieder funkcijas grafikam
1. Veidojam konspektu MG 190.lpp.
2. Skolēni pilda uzdevumus MG 4.51., 4.53. (191.)
4. (3.)
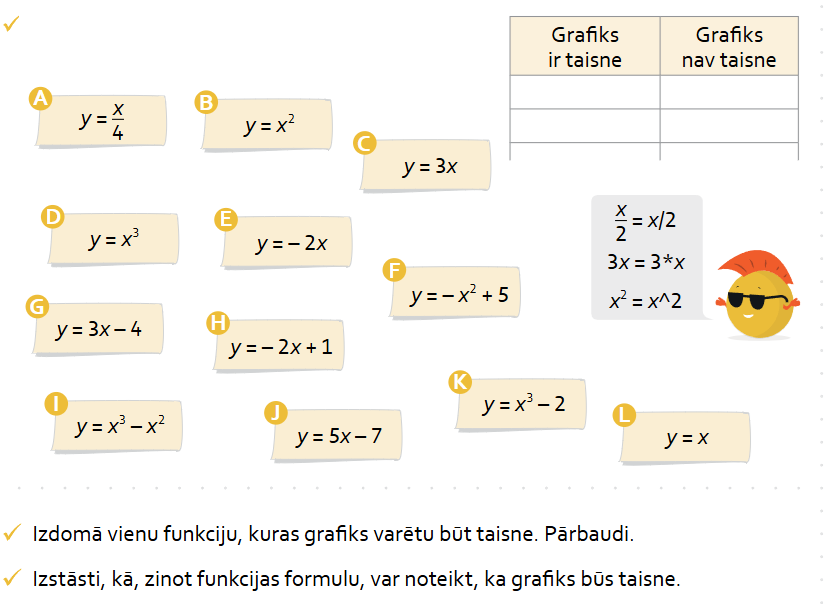
SR. Atpazīst funkciju formulas, kuru grafiks ir taisne
1. Pildām pāros uzdevumu, izmantojot vietni Desmos | Graphing Calculator
Secinājumu ieraksta pierakstos.
6. (5.)
SR. Konstruē lineāras funkcijas grafiku
1. Uzrakstām soļus, kā konstruēt lineāras funkcijas grafiku
2. Skolēni pilda uzdevumus MG 4.56. (192.)
7. (1.) - 20. janvāris
SR. Nosaka, vai funkcija ir augoša vai dilstoša, vai nemainīga
1. Pārliecināmies, ka mākam uzkonstruēt lineāras funkcijas grafiku
2. Noskaidrojam, kā pēc grafika var noteikt, vai funkcija ir augoša vai dilstoša, vai nemainīga
3. Noskaidrojam, kā pēc formulas var noteikt, vai funkcija ir augoša vai dilstoša
4. MG uzdevumi: 4.41., 4.42. (188.)
8. (2.)
SR. nosaka grafiku krustpunkta koordinātas
Uzdevums no MG 4.69. (196.)
Formatīvās vērtēšanas darbs (grafika konstruēšana)
9. (3.)
SR. nosaka grafika krustpunkta ar asīm koordinātas
Uzdevums no MG 4.70. (196.)
8. (4., 5.)
SR. noskaidro kā pēc formulas var noteikt grafika novietojumu
Skolēni veic praktiskus uzdevumus, izmantojot vietni desmos.com/calculator un formulē secinājumus par grafika novietojumu koordinātu plaknē
9. (1.) - no 27.janvāra
SR. Nosaka, kurā punktā grafiks krusto y asi. Nosaka, kuru funkciju grafiki ir paralēli
Pārrunājam formatīvā vērtējuma kļūdas.
Atkārtojam praktiskajā darbā noskaidroto.
Uzdevums:
1. Uzraksti, kuros piemēros dotas paralēlu grafiku formulas.
2. Uzraksti, kurā punktā grafiks krustos y asi.
3. Uzraksti, vai grafiks ir augošs vai dilstošs.
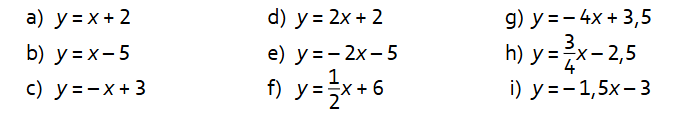
4. Konstruē grafiku: y = – 5x + 7
10. (2.)
SR. Atbild uz jautājumiem, izmantojot procesa attēlojumu ar grafiku
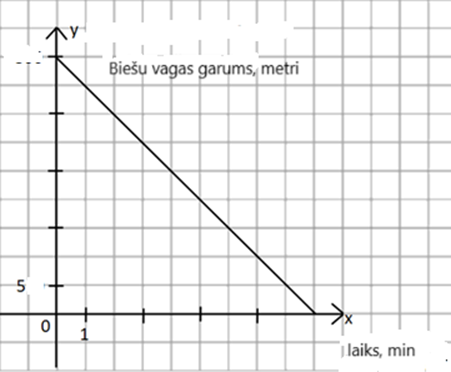
a) Nosaki biešu vagas garumu pirms to sāka ravēt
b) Nosaki, par cik metriem samazinās vagas neizravētās daļas garums katru minūti
c) atliec punktu uz grafika, kas parāda, cik gara ir vagas neizravētā daļa pēc tam, kad tā 7 minūtes ir ravēta
d) Aprēķini, par cik metriem ir samazinājusies vagas neizravētā daļa 7 minūšu laikā
e) Uzraksti formulu, kas izsaka neizravētās vagas
daļas garumu y (metri) pēc x ravēšanas minūtēm. Veic pārbaudi!
11. (3.)
SR. Pārliecinās par gatavību pārbaudes darbam
Izvērtē apgūtās prasmes izmantojot SR tabulu
Pārliecinās par prasmēm, pildot uzdevumus
Lin_funkc_petisana.flipchartSR7_funkcijas_ar_teoriju_un_piemeriem.pdf