1. (1.). no 17. februāra
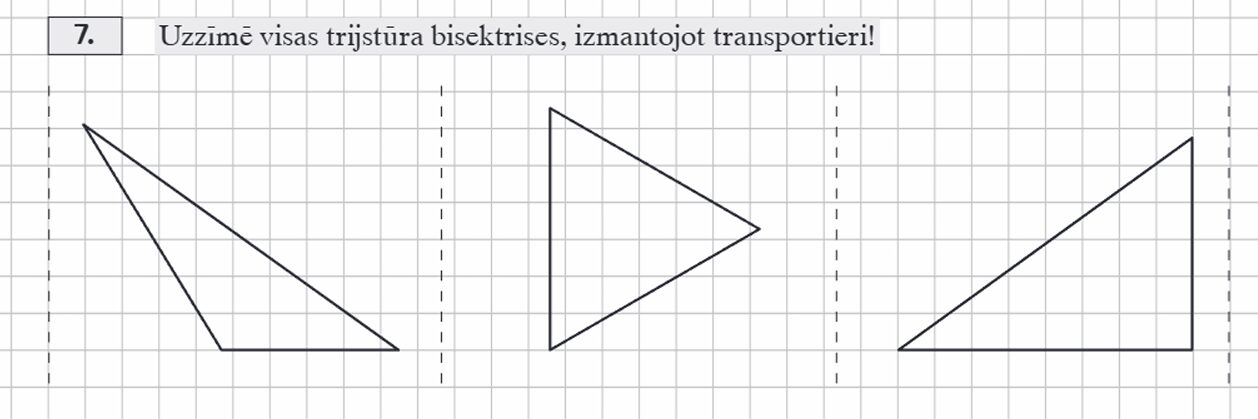
SR. Zīmē trijstūra leņķa mediānu. Lieto zīmējumā apzīmējumus, kas ļauj atpazīt mediānu. Aprēķina nogriežņu garumu, izmantojot mediānas īpašību.
1. Iepazīstamies ar trijstūra mediānas jēdzienu: MG 24.lpp.
2. Pildām uzdevumus
Nosauc katrā zīmējumā mediānu

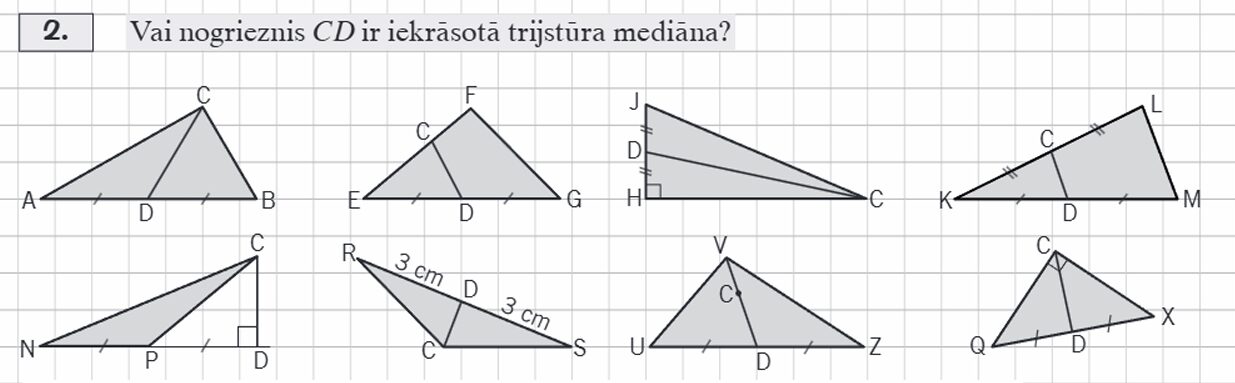
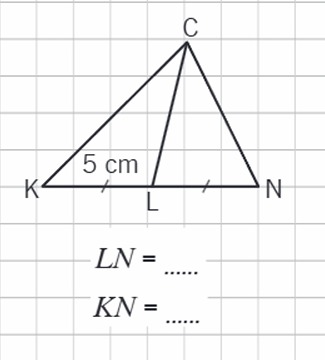 | 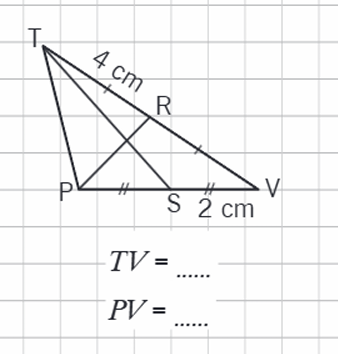 |

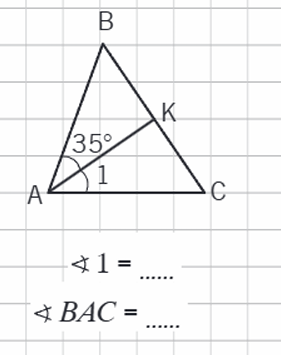
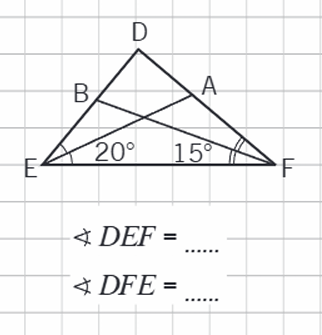
2. (2.).
SR. Zīmē trijstūra leņķa bisektrisi. Lieto zīmējumā apzīmējumus, kas ļauj atpazīt bisektrisi. Aprēķina leņķus, izmantojot bisektrises īpašību.
1. Iepazīstamies ar trijstūra bisektrises jēdzienu: MG 24.lpp.
2. Pildām uzdevumus
Nosauc katrā zīmējumā bisektrisi

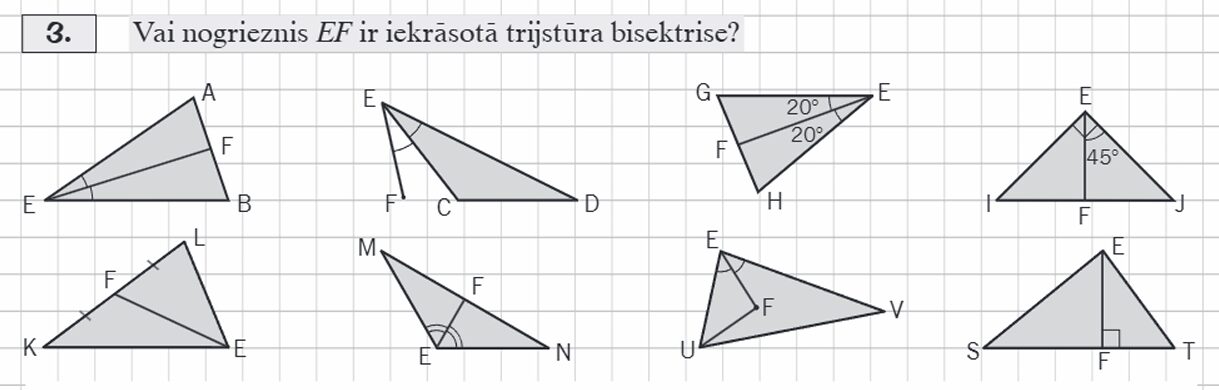
 |  |
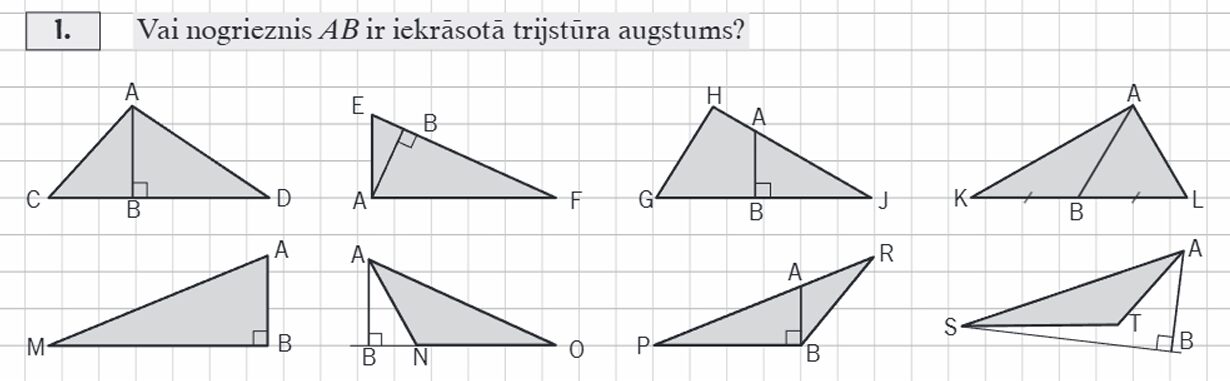
3. (3.).
SR. Atpazīst augstumu šaurleņķa, platleņķa un taisnleņķa trijstūros. Zīmē trijstūra augstumu. Lieto zīmējumā apzīmējumus, kas ļauj atpazīt augstumu.
1. Iepazīstamies ar trijstūra augstuma jēdzienu: MG 25.lpp.
2. Pildām uzdevumus
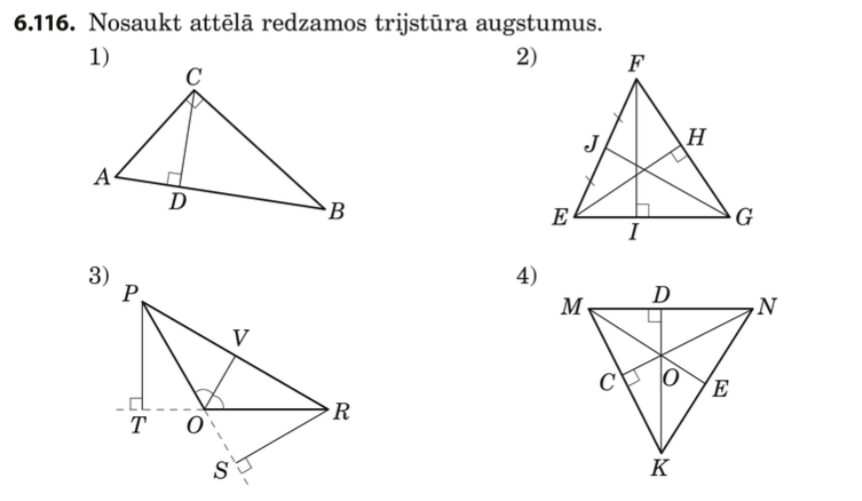
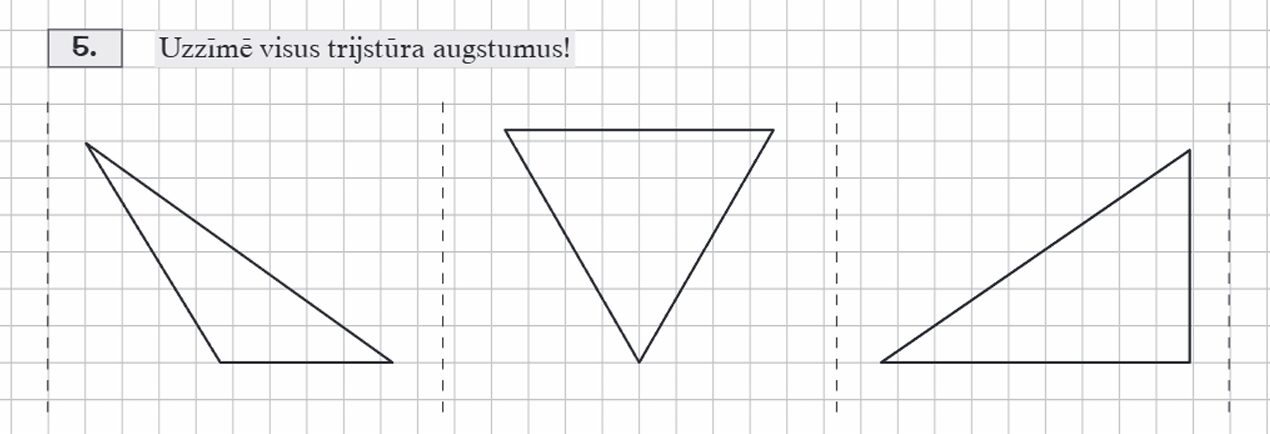
4., 5. (4., 5.).
SR. Zīmē trijstūra augstumu no platleņķa trijstūru šauro leņķu virsotnēm.
1. Skolēni pilda uzdevumi.lv darbu (%): izveidojot 3. un 5. uzdevumu nosacījumiem atbilstošus zīmējumus uz iedotās lapas.
2. Mācāmies zīmēt platleņķa trijstūrus un novilkt augstumus no šauro leņķu virsotnēm. Uzrakstām soļus kā atgādni augstuma zīmēšanai. No 8:18
Tavaklase.lv - Kā konstruēt augstumu, bisektrisi un mediānu un vidusperpendikulu
3. Analizējam pārbaudes darba kļūdas.
6. (1.). - no 24. februāra
SR. Noskaidro vienādsānu trijstūra pazīmes. Izmanto pazīmes vienādsānu trijstūra atpazīšanai.
1. Vai risinot uzdevumus mums ir svarīgi atpazīt trijstūra veidu? Kā atpazīt vienādsānu trijstūri?
2. Atkārtojam vienādsānu trijstūra īpašības izveidojot zīmējumu.
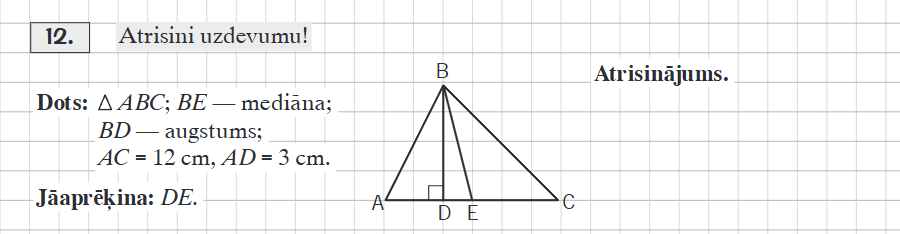
3. No trijstūra virsotnes novilkt mediānu. Minējumi par uzzīmēto nogriezni, minējumu pārbaude. Secinājums.
4. Pārbaudām vai no pamata pieleņķa vilktai mediānai arī piemīt tāda pati īpašība. Secinājums.
5. Formulējam vienādsānu trijstūra pazīmes:
Ja trijstūra ........................................................, tad trisjtūris ir vienādsānu
6. Atpazīstam trijstūra veidu, pamatojot secinājumu: MG 6.18. (76.), 6.22. (77.)
7. Aplūko zīmējumus, kopā ar blakussēdētāju atrodiet un pamatojiet kļūdas.
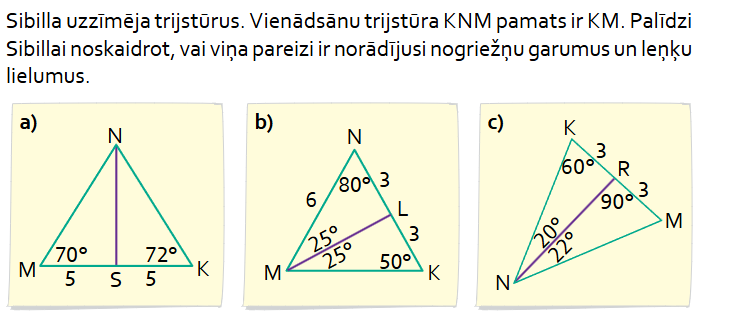
Papilduzdevums: MG 6.190. uzd. 1. daļa (111.)
Pašizvertējums uzdevumi.lv/t
un/vai
Saruna par to, kas vēl būtu jāiemācās
7. (2.).
SR. Formulē vienādmalu trijstūra pazīmes. Aprēķina nogriežņus un leņķus vienādmalu trijstūrī
1. Atkārto vienādmalu trijstūra īpašības. Formulē secinājumu kā vienādmalu trijstūra pazīmi.
Ja ........................................................, tad trisjtūris ir vienādmalu
2. Pārrunājam ģeometrijas uzdevumu risināšanas soļus
4. Risinām uzdevumus: MG 6.51. (83.), 6.53. (83.)
5. Skolēni patstāvīgi risina uzdevumus, salīdzinot izdarīto ar blakussēdētāju: Uzd_trijst_treninam.docx
8. (3.).
SR. Pārliecinās par gatavību pārbaudes darbam
1. Skolēni izvērtē savas prasmes un zināšanas, izmantojot SR tabulu: SR7_sakaribas_trijsturi.docx
2. Kopā veidojam pārskatu par apgūtajām zināšanām
3. Skolēni veido SR tabulā ietvertajām prasmēm atbilstošus zīmējumus. Pieraksta vienādos elementus.
4. Skolēni patstāvīgi risina uzdevumus, salīdzinot izdarīto ar blakussēdētāju: MG 21. (61.), 2.2. (61.), 5.2. (63.), 2.1. (65.), 5.1. (66.)
Papilduzdevumi:
Uzdevumi_trijst_elem_apr.docx
Pašizvertējums uzdevumi.lv/t
un/vai
Saruna par to, kas vēl būtu jāiemācās un kā to varētu darīt