1. (5.) - 31. janvāris
SR. Definē trijstūri, nosauc trijstūra elementus, aprēķina trijstūra perimetru
1. Uzzīmē dažādus trijstūrus
2. Formulē trijstūru definīciju
3. Iepazīstas ar trijstūra pamatelementiem un pierakstu. MG 11.lpp.
4. Risinām uzdevumus: MG 12.lpp.
2. (1.) - no 3. februāra
SR. Atpazīst trijstūra veidu pēc leņķiem (šaurleņķa, platleņķa, taisnleņķa)
1. Pārrunājam pārbaudes darba kļūdas
2. Atkārtojam iepriekšējā stundā apgūto (pretmalas, piemalas, pretleņķi, pieleņķi). Skolēni pilda MG 5.31. (13.)
3. Skolēni izpilda uzdevumi.lv darbu (%)
4. Iepazīstamies ar trijstūru veidiem
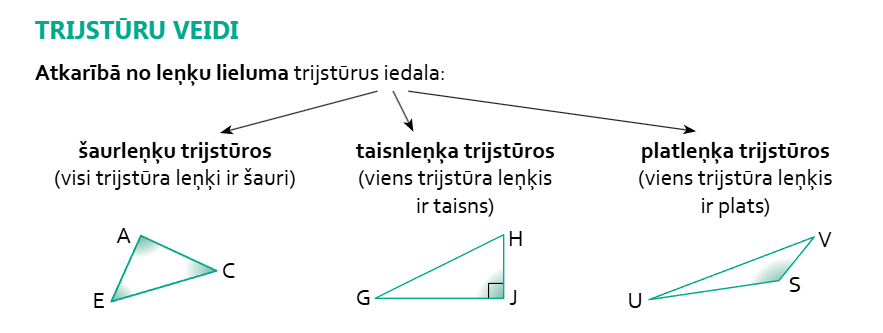
5. Uzdevumi MG 5.39. (14.), 5.46. (15.), 5.47.
3. (2.)
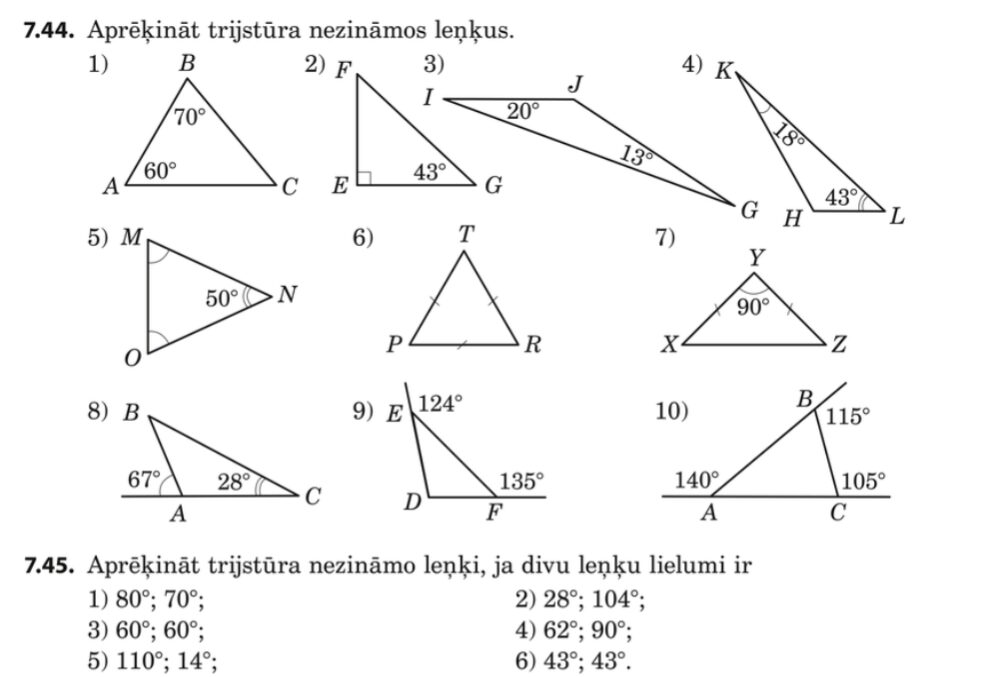
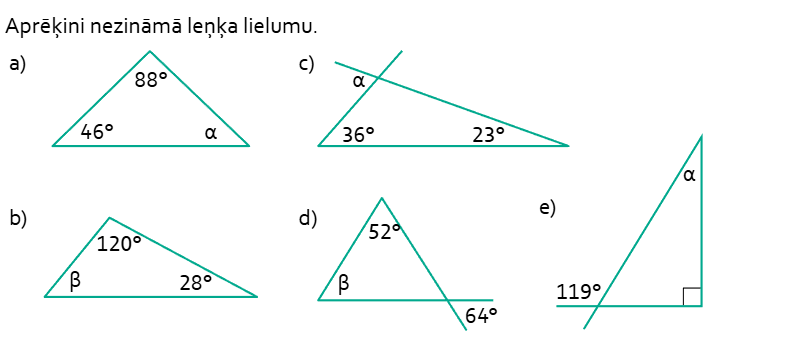
SR. Noskaidro trijstūra leņķu summu. Aprēķina trijstūra leņķa lielumu.
1. Veic praktisko darbu, zīmējot dažādus trijstūrus un izmērot katra trijstūra leņķa lielumus, aprēķina šo leņķu summu, formulē secinājumu.
MG 6.150., 6.151. (105.)
4. (3.)
SR. Atpazīst trijstūra veidu pēc malām (vienādmalu, vienādsānu)
1. Iepazīstamies ar vienādmalu trijstūri un tā īpašībām
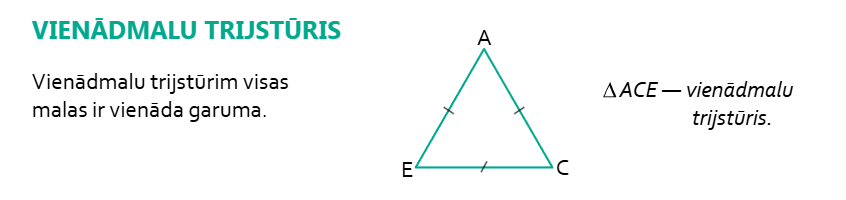
Vienādmalu trijstūrī visi leņķi ir vienādi. Cik liels ir katrs leņķis?
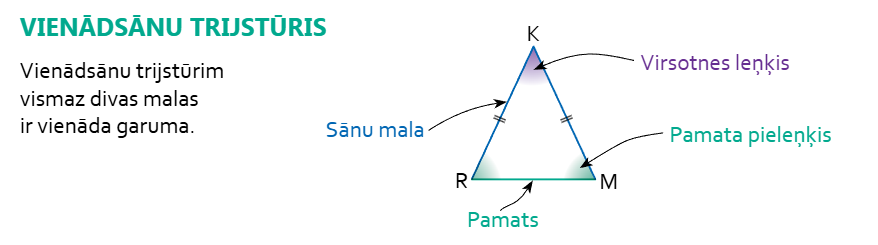
Vienādsānu trijstūrī leņķi pie pamata ir vienādi.
Uzzīmē vienādsānu taisnleņķa trijstūri. Cik lieli ir šī trijstūra šaurie leņķi?
5. (4.)
SR. Nosaka trijstūru garāko (īsāko) malu vai lielāko (mazāko) leņķi
1. Skolēni izsaka minējumus, kā noteikt garāko (īsāko) malu trijstūrī, ja zināmi trijstūra leņķu lielumi; lielāko (mazāko) leņķi, ja zināmi malu garumi.

2. Iepazīstamies ar sakarību starp trijstūra malām un leņķiem: MG 86.lpp.
3. Uzdevumi: MG 6.70. (86.), 87.lpp. uzdevumi.
N.
SR. Zīmē trijstūra leņķa bisektrisi. Lieto zīmējumā apzīmējumus, kas ļauj atpazīt bisektrisi. Aprēķina leņķus, izmantojot bisektrises īpašību.
1. Iepazīstamies ar trijstūra bisektrises jēdzienu: MG 24.lpp.
2. Nosauc katrā zīmējumā bisektrisi

Uzzīmē atbilstošas skices, lieto lielos burtus malu un bisektrises apzīmēšanai. Veido pilnu, korektu risinājuma pierakstu

6. (1.) - no 10. februāra
SR. Nosaka trijstūra eksistences nosacījumus
1. Skolēni izsaka minējumus, kā noteikt vai no dotiem nogriežņiem var izveidot trijstūri. Formulē secinājumus.
2. Skolēni izveido konspektu: MG 18.lpp.
3. Pildām uzdevumus MG 20 lpp. 5.59., 5.64., 5.71.
9. (4.)
SR. Pārliecinās par gatavību pārbaudes darbam
1. Skolēni izvērtē apgūtās prasmes: SR7_trijsturis_24_25.docx
2. Skolēni pilda darba paraugu: Gatav_PD7_trijst.docx
10. (5.)
Pārbaudes darbs:
Kā raksturo trijstūri, izmantojot tā elementus?