1. (4.) - 21. (23.) janvāris
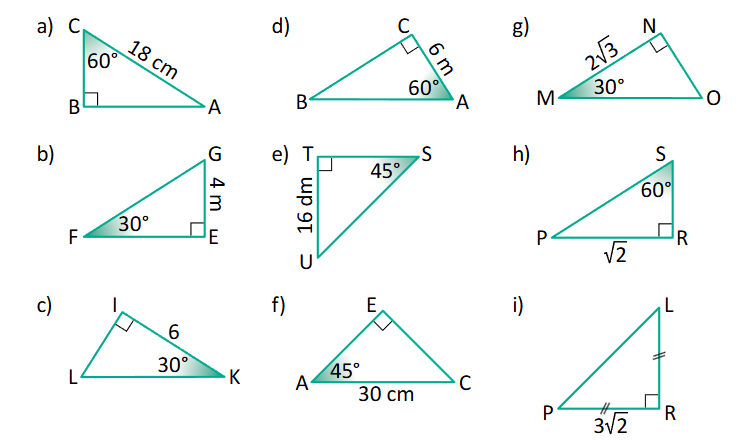
SR: Nosauc taisnleņķa trijstūrī norādītā leņķa pretkateti, piekateti un hipotenūzu. Nosauc leņķi norādītajai pretkatetei, piekatetei
- Izveidojam konspektu
- Pildām MG uzdevumus 224.lpp.
2. (5.)
SR: Gūst priekšstatu par taisnleņķa trijstūra šauro leņķu trigonometriskajām funkcijām
- Veic praktisko darbu MG 225.lpp.
3. (1.) - 27. janvāris
SR: Veido korektu šauro leņķu trigonometrisko sakarību pierakstu taisnleņķa trijstūrim (sasaistot to ar iepriekšējā stundā veikto praktisko darbu)
- Pārbaudes darbu rezultātu izvērtējums
- Pierakstam sakarības trijstūrim PTR (norādes MG 227.lpp.)
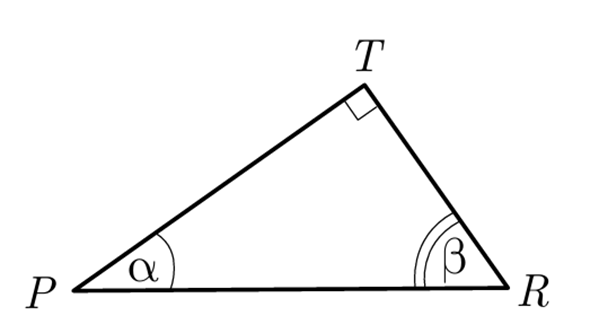
- Pierakstam izvērstas sakarības eksāmena formulu lapā dotajam taisnleņķa trijstūrim. Apskatām, kā formulu lapā doto "pārnest" uz uzdevumā doto trijstūri.
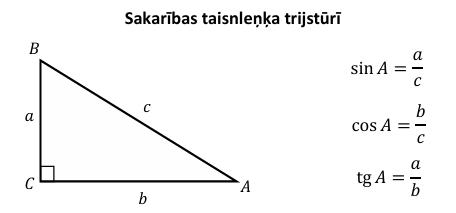
Vingrinājumi MG 1., 2. (228.). Uzdevumi MG 1., 2. (231.)
4. (2.)
SR: Aprēķina taisnleņķa trijstūra šaurā leņķa sinuss (sin), kosinuss (cos) un tangenss (tg) vērtības
Veicam aprēķinus, veidojot izvērstu pierakstu:
- rezultātu pierakstot kā parasto daļu
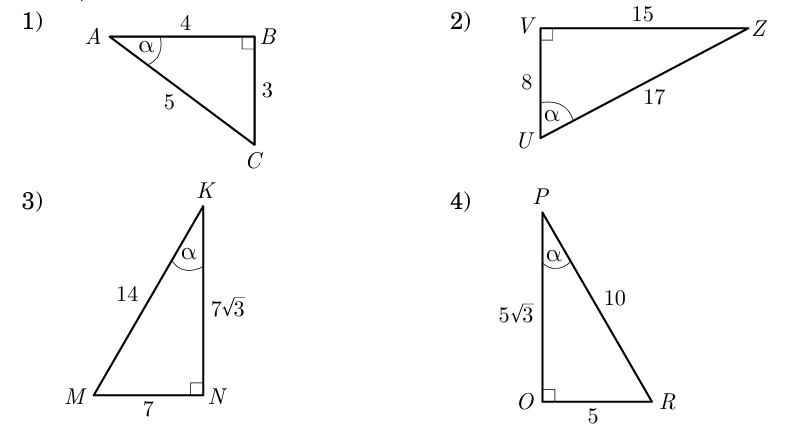
MG 5. vingrinājums (228.)

- atkārtojam decimāldaļu noapaļošanas likumus
- rezultātu pierakstot kā decimāldaļu veicot noapaļošanu
MG 6. vingrinājums (230.)
MG 231.lpp. 4., 5. utt.
5. (3.)
SR: Nosaka taisnleņķa trijstūra šaurā leņķa sinuss (sin), kosinuss (cos) un tangenss (tg) vērtības, izmantojot tabulas. Salīdzina un aprēķina vērtības, izmantojot kalkulatoru. Aprēķina vērtības izteiksmēm.
MPD
Mācāmies lietot tabulu sin, cos, tg vērtību aprēķināšanai. MG vingrinājumi 1., 2., 3., 4. (233.)
Mācāmies lietot kalkulatoru sin, cos, tg vērtību aprēķināšanai. MG vingrinājumi 8. (234.), 9. (235.)
Skolēni pilda uzdevumus MG 236.lpp.
6. (4.)
SR: Aprēķina nezināmo taisnleņķa trijstūra malu, izmantojot šaurā leņķa sinuss (sin), kosinuss (cos) un tangenss (tg) vērtības
Izmantojot eksāmena formulu lapu, nosauc leņķu sin, cos un tg vērtības 30 grādu, 45 grādu un 60 grādu lieliem leņķiem.
Nosaka, kādu trigonometrisko sakarību var izmantot malas aprēķināšanai (vispirms nosauc dotās malas, tad piemeklē atbilstošo attiecību un izdara secinājumu par sakarību).
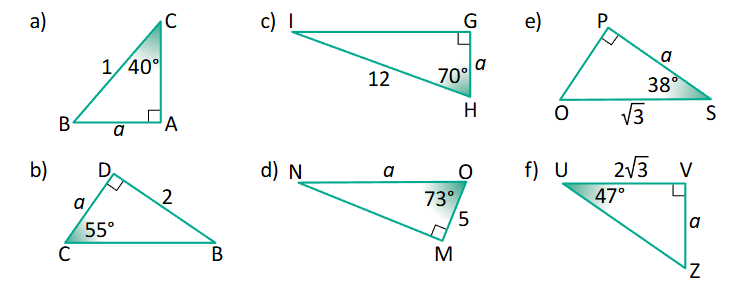
Veidojam pierakstu nezināmās malas aprēķināšanai un veicam aprēķinus
7. (5.)
SR: Aprēķina nezināmo taisnleņķa trijstūra malu, izmantojot tabulā dotās šaurā leņķa sinuss (sin), kosinuss (cos) un tangenss (tg) vērtības
Skolēni risina uzdevumus no MG 284.lpp.
8. (1.)
SR: Aprēķina leņķa sinuss (sin), kosinuss (cos) un tangenss (tg) vērtības, ja zināmas trijstūra malas
Skolēni risina uzdevumu: jāuzraksta atbilstošo malu attiecība, tā jāsaīsina

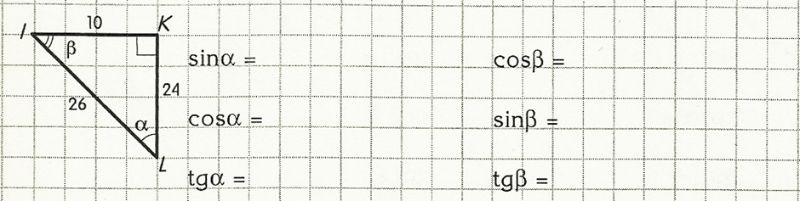
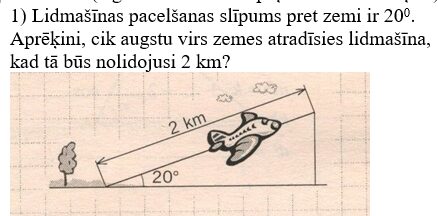
SR: Risina praktiska satura uzdevumus, izmantojot sakarības taisnleņķa trijstūrī (ar kalkulatoru)


8. (2.)
SR: Aprēķina daudzstūra malas un raksturīgos nogriežņus, izmantojot trigonometriskās sakarības
Skolēni risina uzdevumu: uzzīmē zīmējumu atbilstoši aprakstam, parasti jāiezīmē augstums, izveidojot taisnleņķa trijstūri, veic nepieciešamos aprēķinus VAI pilda DL uzdevumus (pamatzināšanas)
Uzdevumi:
1. Vienādsānu trijstūra virsotnes leņķis ir 120°. Augstums, kas novilkts pret sānu malu, ir 6 cm garš. Aprēķināt trijstūra pamata malas garumu.
2.
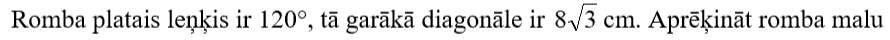
3. Paralelograma īsākā diagonāle ir 12 cm gara, un tā ir perpendikulāra paralelograma īsākajai malai. Paralelograma šaurais leņķis ir 30° liels. Aprēķini paralelograma garākās malas garumu.
4.

9. (3.)
SR: Pārliecinās par apgūtajām prasmēm, risinot dažādus uzdevumus
Skolēni iepazīstas ar SR tabulu: SR_sakar_taisnlenka_trijst_2024_2025.pdf
Skolēni pilda DL: DL_soma_trigonom-1.pdf
10. vai 11. (4. vai 5.)
Pārbaudes darbs
11. ( 5.)